1 INTRODUCTION

Le modèle du Big-Bang suppose que l'univers a été formé à partir de particules agissant entre elles, qui se sont associées pour former des noyaux, puis des atomes, puis des molécules, puis des objets de plus en plus étendus et complexes, donnant naissance à l'arbre entier des êtres vivants, des bactéries aux animaux munis de conscience. Un réductionnisme strict ne peut pas expliquer comment cette évolution a été possible, comment de nouvelles propriétés ont pu émerger et surmonter les sauts d'énergie entre les niveaux.

Notre but est de proposer un modèle mathématique, basé sur la théorie des catégories (cf. Mac Lane [18]), qui justifie un "réductionnisme émergentiste" au sens de Mario Bunge [3]. Cet article présente des résultats que nous avons développés dans une série de publications depuis 15 ans, dont un sommaire peut être trouvé dans notre site Internet. Il repose sur le principe de multiplicité (généralisant le "principe de dégénérescence" de Edelman [9]) qui affirme l'existence d'objets complexes, appelés objets multiface, qui peuvent "balancer" entre plusieurs configurations en éléments plus simples. Si une catégorie K satisfait ce principe, nous montrons que n'importe quelle complexification de K le satisfait également, et nous expliquons comment ceci entraîne l'émergence d'objets multiface de plus en plus complexes dont les propriétés ne sont pas réductibles à celles de leurs constituants de niveau inférieur, mais dépendent d'une façon précise de la structure globale de ce niveau inférieur (d'où un genre de délocalisation contrôlée).

Ce modèle peut être appliqué aux systèmes naturels parce que les lois de la physique quantique assurent que le principe de multiplicité est satisfait dans la catégorie des particules et des atomes, de sorte qu'il sera également satisfait dans les systèmes obtenus par évolution de cette catégorie. Il donne un sens précis au fait que les propriétés quantiques sont à l'origine de l'émergence de processus d'ordre supérieur jusqu'à la conscience, comme divers auteurs l'ont proposé (par exemple, Hameroff et Penrose [16], Pribram [23],…).

La section 2 est consacrée au modèle mathématique général ; les outils catégoriques sont seulement brièvement définis et nous renvoyons à la section 4 pour des définitions précises des mots suivis d'un astérisque. Il est ensuite appliqué à l'évolution des systèmes naturels tels que les systèmes biologiques et neuraux, modélisés par les Systèmes Evolutifs à Mémoire (SEM), qui sont des systèmes autonomes anticipatifs (au sens de Rosen [24], cf. également [7]).

Dans la section 3, les systèmes cognitifs, modélisés par le SEM des neurones, sont étudiés plus en détail, soulignant le signification du principe de multiplicité dans ce cas. En particulier, nous décrivons comment les animaux supérieurs deviennent capables d'enregistrer leurs expériences et de les classifier pour développer une sémantique. L'existence d'une telle sémantique permet le développement, à partir de la naissance, d'un sous-ensemble du SEM, le noyau archétypal, dont les objets multiface intègrent toutes les expériences sensorielles, émotives, motrices et les stratégies qui leur sont associées ; ses liens sont forts, rapidement activés, graduellement renforcés et sont ainsi à la base de la notion d'individu.

Nous caractérisons la conscience comme le processus qui, se fondant sur ce noyau archétypal, intègre les dimensions temporelles : (i) Un nouvel événement déclenchera une recherche sémiotique dans le noay archétypal qui, par balancements entre configurations d'objets multiface, mène à la formation d'un paysage étendu "holiste", dont les objets sont les perspectives temporelles de l'événement et de ses réflexions internes ; (ii) ce paysage étendu permet d'exécuter un processus de rétrospection jusque dans les niveaux inférieurs du passé proche pour trouver, par abduction, les causes de l'événement actuel, et (iii) un procédé de prospection (orienté vers le futur) pour choisir des stratégies à long terme permettant de répondre de la manière la plus adaptative.

L'état d'un système, tel qu'un système biologique, social ou neural, à l'instant t est modélisé par une catégorie* : ses objets représentent les composants (de tous niveaux) du système, et ses morphismes (appelés liens) leurs interactions dans le système aux environs de ce temps. Ces liens peuvent représenter des relations structurales plus ou moins stables telles que des relations causales ou topologiques (par exemple, desmosomes entre cellules adjacentes), des canaux transmettant une information, des contraintes spatiales ou énergétiques, ou des interactions provisoires entre deux composants. La loi de composition associe à 2 liens successifs leur interaction cumulative ; elle est associative et ainsi elle permet de distinguer parmi les chemins de liens successifs ceux qui correspondent à des interactions cumulatives équivalentes.

Les changements entre états successifs du système sont représentés par des foncteurs* partiels entre les catégories correspondantes, de sorte que le système est représenté par un Système Evolutif* K, à savoir une suite de catégories K_t représentant les états du système aux dates successives t d'une échelle de temps (finie ou infinie) T, et des foncteurs partiels entre elles, appelés transitions (Ehresmann et Vanbremeersch [10]).

Un sous-système* de K est un système évolutif tel que son échelle de temps S est incluse dans T, qu'à chaque date s de S sa catégorie est une sous-catégorie de K_s et ses transitions sont des restrictions de celles de K

Dans les systèmes naturels, les objets sont répartis en différents niveaux de complexité, chaque niveau satisfaisant ses propres règles. Il y a des liens internes à un niveau, mais également des liens interniveaux. Un objet du niveau n+1 est un agrégat d'objets du niveau n, liés par des interactions fortes entre eux qui déterminent leur cohésion dans l'agrégat. Par exemple dans un atome, le noyau et les électrons sont unis par les forces d'attraction entre les électrons et les protons, et les forces de répulsion entre les électrons et l'intérieur du noyau ; ainsi l'atome a une organisation interne dépendant de sa configuration électronique.

Comment pouvons-nous modéliser une telle organisation hiérarchique dans une catégorie ? L'idée est d'utiliser l'opération bien connue de colimite (Kan [17]), de sorte qu'un agrégat N soit modélisé par la colimite d'un pattern d'objets liés représentant son organisation interne.

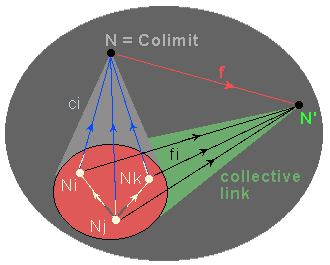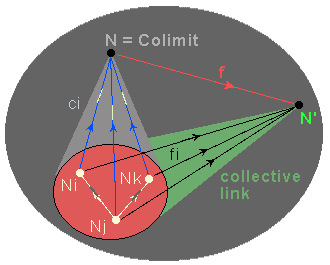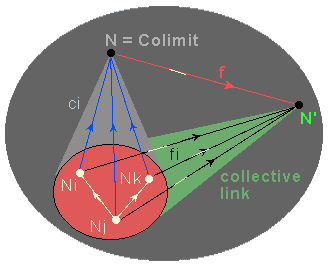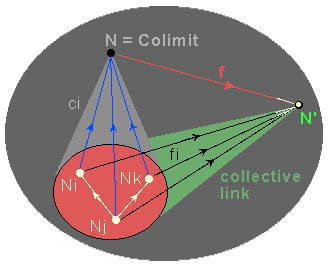Un pattern* P est défini comme une famille d'objets N_i de la catégorie et de liens distingués entre eux. Un lien collectif* de P vers un objet N' est une famille de liens (f_i: N_i ® N') corrélés par les liens distingués du pattern. Les liens collectifs représentent des interactions cohérentes (contraintes, transferts d'énergie ou d'information) effectuées par tous les N_i agissant de manière coopérative grâce à leurs liens distingués, interactions qui ne pourraient pas être réalisées par les objets du pattern agissant individuellement.

Un pattern P peut avoir les liens collectifs vers plusieurs objets. P a un agrégat si, parmi ces liens collectifs, il y en a un "optimal", c'est-à-dire s'il en existe un (c_i: N_i ® N) par lequel tous les autres se factorisent. En termes catégoriques, ceci signifie que N est la colimite* de P ; nous disons également que N recolle (Paton [22]) le pattern P ; ou, vu dans la direction opposée, que P est une décomposition de l'objet complexe N. La colimite a des propriétés localisées en tant que donnant une représentation objectale du pattern qu'elle recolle et qui acquiert ainsi une stabilité dynamique ; mais elle a également des implications "globales" pour son environnement par suite de sa "propriété universelle" de factoriser chaque lien collectif.

Une colimite ne doit pas être confondue avec la simple somme* des objets du pattern (pris sans leurs liens distingués), qui ne tient pas compte de leur comportement cohérent. Par exemple, dans la catégorie des objets quantiques (particules jusqu'aux atomes) avec leurs interactions, une superposition ou un "entanglement" est une colimite, alors qu'un état mélangé est seulement une somme.

Certaines interactions entre objets complexes proviennent directement d'interactions distribuées entre les constituants du niveau inférieur de ces objets ; en termes d'énergie elles n'ajoutent rien de nouveau à ce qui est connu à ce niveau inférieur. Dans le modèle catégorique, elles sont modélisées par les liens simples : si N est la colimite de P et de N' la colimite de P', un lien (P,P')-simple* de N à N' est un lien qui recolle une gerbe de liens de P à P' ; une telle gerbe* est une famille de liens des objets N_i de P vers les objets N'_j de P', bien corrélés par les liens distingués des deux patterns, de sorte qu'ils envoient collectivement des informations cohérentes à P'.

En gros, un lien simple "institutionnalise" la gerbe, sans ajouter 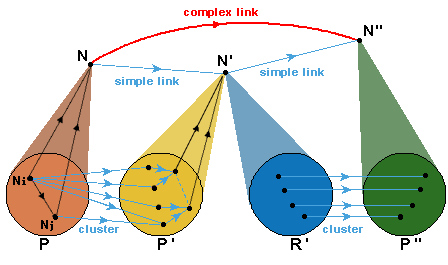aucune information qui n'est pas accessible au niveau des patterns. Par exemple, en embryologie, l'induction d'une population de cellules par une autre correspond à la formation d'un lien simple. Un composé de liens simples recollant des gerbes adjacentes est un lien simple.

Cependant dans certaines catégories il existe les liens qui ne sont pas simples bien que composés de liens simples, mais recollant des gerbes non adjacentes ; on les appelle des liens complexes*. Ceci est possible s'il existe des objets N' qui sont la colimite de deux patterns non équivalents*, disons P' et R' ; de tels objets sont dits multiface, et le passage entre P' et R' s'appelle un balancement complexe. Pendant l'évolution du système, il permet que P' et R' échangent leur rôle fonctionnel, bien qu'il n'y ait aucune interaction localisée distribuée parmi leurs constituants.

Nous verrons que l'existence de balancements complexes a des conséquences importantes pour le problème de l'émergence. Ainsi nous avons introduits (Ehresmann & Vanbremeersch [12]) :

Définition. Une catégorie vérifie le Principe de Multiplicité (abrégé en MP) si certains de ses objets sont multiface, c'est-à-dire s'il existe des patterns non équivalents admettant la même colimite. Un système évolutif satisfait le MP si ses catégories d'états satisfont le MP.

Si la catégorie satisfait le MP, il existe des liens complexes. Un lien complexe de N à N" est obtenu comme composé d'un lien (P,P')-simple de N à un objet multiface N' avec un lien (R',P")-simple de N' à N", où P' et R' sont deux décompositions non équivalents de l'objet multiface N'. Il représente des propriétés qui ne dépendent pas seulement des interactions entre les objets des décompositions P et P" de N et de N", mais également, d'une façon plus compliquée, sur les propriétés des décompositions P' et R' de l'objet multiface intermédiaire N' et sur l'existence d'un balancement complexe entre P' et R' (e.g. représentant une transformation énergétique). Ainsi ce lien a des propriétés émergentes globales relativement aux décompositions de N et de N" donnés par P et P", ces nouvelles propriétés dépendent de la structure de niveau inférieur, mais prise dans sa globalité et pas seulement localement au travers des constituants de N et de N". Un composé de liens complexes est un lien complexe (ou, rarement, un lien simple).

Les lois de la physique quantique assurent que le MP est satifait dans le système quantique, modélisant le système des particules quantiques et des atomes avec leurs interactions. En effet, un atome est représenté par la colimite de n'importe laquelle de ses configurations électroniques en orbitales atomiques, et il y a des balancements complexes entre les configurations liées à différents niveaux d'énergie. De ceci, nous déduirons (cf. Section 2,6) que le MP est également satisfait dans les systèmes naturels, puisqu'ils sont obtenus à partir de sous-systèmes du système quantique par le procédé de complexification. Dans de tels systèmes concrets un balancement complexe correspond généralement à une transformation d'énergie ; il peut se voir comme une fluctuation aléatoire dans l'organisation interne d'un objet qui ne modifie pas sa fonctionnalité au niveau plus élevé : plusieurs micro-états peuvent mener au même macro-équilibre. Un exemple d'un tel balancement est le passage entre génotypes avec des allèles différents mais menant au même phénotype.

Un système hiérarchique est un Système Evolutif dans lequel chaque catégorie est hiérarchique, c'est-à-dire ses objets sont répartis en une suite de niveaux de complexité 0, 1,…, m, de sorte que chaque objet N du niveau n+1 soit la colimite d'au moins un pattern d'objets liés N_i du niveau n. Dans ce cas, puisque N est la colimite d'un pattern P d'objets liés du niveau n et que chacun de ces N_i est la colimite d'un pattern P_i, l'objet N est la colimite 2-itérée de (P,(P_i)), et (P,(P_i)) est appelé une ramification de N de longueur 2. La ramification représente une organisation interne de N impliquant deux niveaux, qui détermine en 2 étapes les liens de N aux autres objets de la catégorie.

Plus généralement, nous définissons inductivement une colimite k-itérée et une k-ramification d'un objet A de niveau supérieur à k. En gros, A a une sorte de structure fractale, dont les composants à chaque étape intermédiaire sont eux-mêmes ramifiés, mais avec de plus des corrélations entre ces ramifications représentées par les liens distingués "horizontaux" entre les composants à chaque niveau.

Si le MP est satisfait, un objet multiface A a une multiplicité de ramifications qui rendent cette structure très flexible. En effet, si nous pensons qu'une décomposition de A attribue des valeurs particulières ("variables") à certaines caractéristiques de A, comme les fentes dans un "cadre" (au sens de Minsky [21]), une k-ramification amplifie le choix puisque des choix successifs peuvent être faits à chacune de ses k étapes. Le nombre de ramifications non équivalentes de A arrivant à un niveau inférieur k donne une mesure de la flexibilité de A, dans le sens du nombre de ses organisations internes fonctionnelles jusqu'à ce niveau ; il pourrait être appelé la k-entropie de A.

Dans un système hiérarchique, le niveau d'un objet N n'est pas une bonne mesure de sa complexité "réelle" ; celle-ci est mesurée par l'ordre de N, qui est le plus petit p tel qu'il existe un pattern d'objets liés du niveau p admettant N comme colimite. Et N est dit q-réductible pour tout q inférieur ou égal à son ordre.

Par définition, tout objet du niveau n+1 est n-réductible. Quand est-il p-réductible, pour un p inférieur à n ? Pour répondre, nous devons classifier avec plus de précisions les liens : Un lien entre deux objets N et N' de niveau n+1 est n-simple s'il recolle une gerbe entre deux patterns de niveau inférieur égal à n. Il est n-complexe si c'est le composé de liens n-simples recollant des gerbes non adjacentes, sans être lui-même n-simple. De plus, il pourrait également exister des liens qui ne sont ni n-simples ni n-complexes, et qui représentent des contraintes indépendantes des niveaux inférieurs.

Alors le résultat suivant a été prouvé dans Ehresmann et Vanbremeersch [12] :

Théorème. Un objet N de niveau n+1 est (n-1)-réductible s'il admet pour décomposition un pattern d'objets N_i de niveau n dans lequel les liens distingués sont des liens (n-1)-simples recollant des gerbes adjacentes entre the N_i. Autrement, N peut ne pas être (n-1)-réductible. Ce résultat s'étend aux niveaux inférieurs.

Ce théorème montre les limites du programme réductionniste strict qui suppose que n'importe quel objet est réductible en une seule étape, au niveau le plus bas, c'est-à-dire est d'ordre 0. Cependant dans la plupart des systèmes hiérarchiques naturels, il y a une possibilité de réduction à des niveaux plus bas, mais en plusieurs étapes et avec émergence à chaque niveau de nouvelles propriétés reflétant les propriétés holistiques du niveau précédent. De tels systèmes sont k-basés, pour un certain k, dans le sens que les liens de niveau n+1 sont n-simples ou n-complexes, pour tout n > k, c'est-à-dire qu'aucune contrainte externe n'est rajoutée dans la "montée" à partir du niveau k. Dans un tel système non seulement chaque objet est reconstruit par étapes à partir du niveau k par une ramification (ce qui est vrai dans n'importe quel système hiérarchique), mais les liens peuvent également être reconstruits par étapes puisqu'ils recollent des gerbes du niveau juste inférieur, ou sont des composés de tels liens. Cependant cette reconstruction dépend non seulement des propriétés "locales" des composants de niveau k de l'objet ou du lien (comme l'exigerait un programme réductionniste), mais également de la structure "globale" de chaque niveau successif. Ainsi il y a vraiment émergence de nouvelles propriétés par rapport aux composants de l'objet.

En effet, nous avons vu ci-dessus que les propriétés d'un lien k-complexe de N à N" dépendent non seulement de celles des patterns que N et N" recollent, mais également de celles des objets multiface intermédiaires intervenant dans sa construction ainsi que de leurs balancements complexes ; elles émergent donc de la structure globale du niveau k.

Maintenant soit A un objet du niveau k+2. Il peut être reconstruit à partir du niveau k comme colimite 2-itérée d'une ramification (R,(P_i)) ; mais, si certains des liens de R sont complexes, il s'ensuit qu'ils imposent également à A des propriétés émergeant de la structure globale du niveau k, et ne reflétant pas seulement les propriétés locales des composants de niveau inférieur de A.

Nous pouvons parler d'un "réductionnisme émergentiste" (précisant ainsi la notion proposée par Mario Bunge [3]). En particulier, pour les systèmes 0-basés (i.e. si k = 0), le langage non linéaire du système sera entièrement décodé à partir des termes primitifs, à savoir les objets du niveau 0 avec leurs interactions, et de la "syntaxe" qui indique comment ils se recollent ensemble pour construire progressivement les objets et les liens des niveaux plus élevés en plusieurs étapes avec, à chaque niveau, émergence de nouvelles propriétés dépendant de la structure globale du niveau précédent.

De tels systèmes hiérarchiques peuvent être construits par le procédé suivant.

Cette situation se produit dans les systèmes évolutifs naturels, qui sont basés sur des sous-systèmes du système quantique. Durant l'évolution ou le développement d'un système naturel, le changement d'états est contrôlé par les processus de "naissance, mort, scission, collision" (Thom [25]) ; pour une cellule, endocytose, exocytose, décomposition et synthèse de macromolécules. Ceci est modélisé par le processus de complexification d'une catégorie relativement à une stratégie.

Une stratégie S sur une catégorie K est la donnée de : éléments externes "à absorber" ; objets ou liens de la catégorie "à supprimer" ou "à décomposer" ; patterns sans colimite "à recoller", de sorte qu'une colimite soit ajoutée ; cônes "à transformer en cônes colimite", de sorte que le sommet du cône devienne une colimite de sa base.

La complexification de K par rapport à la stratégie S est une catégorie dans laquelle les objectifs de S sont réalisés de la manière la plus économique (solution d'un problème universel). Si la catégorie modélise un système naturel, économique signifie avec le moindre coût matériel, temporel, informatique et énergétique.

La complexification a été explicitement décrite (Ehresmann et Vanbremeersch [10]) : Ses objets sont : tous les objets de K non supprimés par S, les éléments à absorber et, pour chaque pattern P à recoller, un nouvel objet colim P devenant sa colimite, qui émerge par intégration du pattern en une unité d'ordre supérieure. Ses liens sont de deux types : liens simples recollant des gerbes entre les patterns de K, et liens complexes qui sont des composés des liens simples recollant des gerbes non adjacentes. Dans les termes de Farre [14], nous pouvons penser à P comme le cycle causal interne, alors que l'émergence de colim P le sépare de son contexte en lui donnant un caractère objectal.

Nous avons vu que l'émergence de nouvelles propriétés exige l'existence d'objets multiface. Maintenant nous avons :

Théorème. Si K satisfait le principe de multiplicité, il en est de même pour toute complexification de K.

Le processus de complexification peut être itéré, et, si K satisfait le MP, ses complexifications successives mènent à l'émergence d'une hiérarchie d'objets complexes d'ordre croissant de complexité, avec des propriétés émergeant à chaque niveau. Ainsi le MP explique comment une émergence "réelle" peut se produire.

Corollaire. Le MP est satisfait dans le système quantique et dans les systèmes naturels obtenus par complexifications successives de ses sous-systèmes.

En effet, nous avons vu dans la Section 2,3 que la physique quantique implique que le MP est satisfait dans le système quantique. Du théorème ci-dessus il découle que le MP est également satisfait dans des complexifications successives de ses sous-sysèmes, de sorte qu'elles mènent à une hiérarchie d'objets de plus en plus complexes, modélisant l'évolution de tout l'univers physique. La plupart des systèmes naturels, en particulier les systèmes biologiques, neuraux ou sociaux, sont obtenus de cette façon.

Remarquons que, dans le système quantique, un balancement complexe résulte d'un processus quantique. Dans des complexifications successives, il y aura encore des objets multiface admettant des balancements complexes. Comme nous avons vu ci-dessus, ils émergent de la structure globale des niveaux inférieurs, par conséquent sont ultimement basés sur les propriétés des processus quantiques, tels que la superposition et la non-localisation. Mais qu'ils puissent être reconstruits à partir d'une telle base ne signifie pas que les objets multiface "ont" des propriétés quantiques ; en fait leurs macro-propriétés sont classiques. Ainsi nous différons de l'interprétation d'Aerts et al. [1] qui parlent de "quantum-mechanical properties" pour les interactions cognitives. En fait, leurs exemples sont facilement traduits en disant que les objets qu'ils considèrent (par exemple le concept "chat") sont multiface, d'où les propriétés qu'ils décrivent.

Les systèmes naturels autonomes, tels que les systèmes biologiques, neuraux ou sociaux, sont obtenus par des complexifications successives de sous-systèmes du système quantique, comme décrit ci-dessus, de sorte qu'ils satisfont le principe de multiplicité. Ces systèmes sont ouverts, auto-régulés, capables d'enregistrer leurs expériences d'une manière flexible et de s'adapter à leur environnement par la reconnaissance des situations déjà rencontrées et le rappel des meilleures stratégies pour y faire face. Ainsi ce sont des systèmes anticipatifs ("anticipatory systems") au sens de Rosen [24], concept développé par beaucoup d'auteurs, en particulier Dubois (cf. [7]). Cependant nous n'employons pas cette terminologie mais préférons les considérer inversement comme ayant une "mémoire". Dans [11], nous avons présenté un modèle pour ces systèmes, appelé Systèmes Evolutifs à Mémoire (SEM).

Le processus de complexification suppose d'abord qu'une stratégie a été choisie sur la catégorie à complexifier. Dans les systèmes autonomes, les stratégies seront choisies d'une façon interne, en tenant compte de l'information venant de l'environnement et de l'état interne. Pour ceci, nous supposons qu'il existe un réseau d'organes internes de régulation, appelés CoRégulateurs (CR). et ces CR participeront au développement d'une mémoire centrale pour enregistrer les différentes expériences.

Plus précisément, un SEM est un système évolutif hiérarchique dont l'architecture est un compromis entre un système parallèle distribué multi-agents, et un réseau associatif hiérarchique. Il a un sous-système hiérarchique, appelé la mémoire et noté Mem qui se développe au cours du temps pour enregistrer et stocker les différentes situations rencontrées et les stratégies utilisées, de sorte qu'elles puissent être rappelées plus tard. Sa dynamique est modulée par la coopération et/ou la compétition entre un réseau de sous-systèmes, les CoRégulateurs (CR).

Chaque CR opère, à son propre niveau de complexité et avec sa propre temporalité, un processus d'apprentissage par essais/erreurs, en utilisant son accès différentiel à la mémoire centrale au développement de laquelle il participe. À un moment donné, un CR ne peut acquérir que des informations partielles sur le système et sa situation, informations plus ou moins limitées selon le niveau de complexité de ses objets (appelés ses agents) ; par exemple, dans un système neural, un CR inférieur peut ne percevoir qu'un certain attribut (tel que la couleur ou la forme) tandis que des CR associatifs plus élevés ont une plus grande base, pouvant contrôler plusieurs CR inférieurs. Ces informations forment son paysage actuel*.

Nous pouvons penser à un CR comme étant un observable, dont le paysage est l'espace d'observation contenant les mesures particulières qu'il peut faire. Mais le CR ne "mesure" pas seulement ; il a également un rôle "actif" dans le choix d'une stratégie pour répondre à l'information qu'il a reçue. Ceci pourrait être comparé à la notion d'une transaction dans l'interprétation transactionnelle de la physique quantique (Cramer [5]) : le CR envoie une "question" ("offer wave") à la mémoire qui active d'anciennes expériences semblables et les stratégies utilisées alors avec leurs résultats, celles-ci sont reflétées dans le paysage ("confirmation wave"), éventuellement comparées, et la "transaction" est réalisée par le choix d'une stratégie et l'envoi des commandes correspondantes aux effecteurs. Si la commande concerne un objet multiface, sa réalisation peut choisir n'importe laquelle de ses décompositions (à comparer à la "réduction" de la fonction d'onde, ou "collapse of a wave packet"). Quelle décomposition est utilisée dépendra du contexte, par exemple des stratégies simultanément choisies par les autres CR.

En effet, chaque CR opère indépendamment sur son paysage, mais tous les CR partagent les ressources communes du système. Ainsi les stratégies des différents CR sont répercutées au système entier où elles doivent être rendues cohérentes et respecter les contraintes structurales et temporelles de chaque CR. Ceci est réalisé par un processus d'équilibration, appelé "le jeu entre les stratégies". Il peut avoir comme conséquence des fractures pour certains CR, s'il y a des incompatibilités qui ne peuvent pas être résolues.

Ce jeu repose fortement sur l'existence de balancements complexes, qui permettent de réaliser les diverses commandes d'une stratégie en choisissant parmi leurs ramifications celles qui donnent l'ensemble le plus cohérent. Il en résulte une dialectique entre CR hétérogènes de par leur temporalité et leur complexité, basée sur des boucles fonctionnelles, qui peut expliquer l'émergence de phénomènes complexes adaptatifs.

Maintenant concentrons-nous sur un système cognitif, correspondant au développement et au fonctionnement du système nerveux d'un animal supérieur. Il est modelé par le SEM des neurones, obtenu par complexifications successives de la catégorie des neurones définie comme suit : ses objets sont les neurones, les liens sont des classes de chemins synaptiques entre neurones, deux tels chemins étant identifiés s'ils sont fonctionnellement équivalents, c'est-à-dire s'ils ont la même force. Comme cette catégorie est elle-même la complexification d'un sous-système du système quantique, elle satisfait le MP ; par conséquent il en est de même pour le MES des neurones obtenu par ses complexifications successives. Voyons ce que ceci signifie dans ce cas.

La réponse d'un système neural à un stimulus simple est l'activation d'un neurone spécialisé particulier ; par exemple, dans les aires visuelles, il existe des cellules "simples" représentant un segment d'une direction donnée, et des cellules "complexes" représentant un angle particulier. Mais des stimuli plus complexes, à quelques exceptions près (par exemple, un neurone activé par une main tenant une banane pour un singe), n'ont pas leur propre "neurone de grand-mère'. Le développement de l'imagerie neuronale semble confirmer l'idée "associationniste" : des stimuli sensoriels complexes, ou des programmes moteurs, sont représentés par l'activation synchronisée de courte durée d'une assemblée spécifique de neurones. Et l'apprentissage consisterait en la formation de telles assemblées synchrones, par le renforcement des synapses entre leurs neurones, selon la règle déjà proposée par Hebb [15] : la force d'une synapse entre deux neurones est renforcée si les deux neurones sont activés en même temps, et diminuée si l'un est activé alors que l'autre ne l'est pas.

Dans notre modèle, une assemblée de neurones est représentée par un pattern P dans la catégorie des neurones Neur. La synchronisation de cette assemblée sera modélisée par l'émergence d'une colimite de ce pattern dans une complexification de Neur ; cette colimite, qui fonctionne comme un "neurone d'ordre supérieur" unique intégrant l'assemblée synchrone, est appelé un neurone de catégorie (ou simplement un cat-neurone). La construction de la complexification détermine ce quels sont les "bons" liens entre les cat-neurones, par conséquent entre les assemblées synchrones de neurones, donnant ainsi une réponse au "binding problem" étudié en neuroscience (cf. von der Malsburg [19]). Le MP étant satisfait, le même cat-neurone peut représenter différentes assemblées synchrones, ce qui explique la flexibilité de la mémoire. Et ceci permet de définir, par des itérations du processus de complexification, des cat-neurones de plus en plus complexes, représentant des assemblées d'assemblées de neurones... correspondant au développement d'objets mentaux et de processus cognitifs d'ordre supérieur.

Ainsi les résultats généraux exposés dans la Section 2 montrent dans quel sens précis les processus cognitifs de n'importe quel niveau sont basés sur des processus quantiques. Remarquons que plusieurs auteurs ont proposé que les processus quantiques soient responsables des processus cognitifs, mais sans décrire exactement de quelle manière. En fait leurs théories peuvent être vues comme reposant sur l'existence de balancements complexes, mais seulement au niveau sous-cellulaire : pour Pribram [23] via les teledendrons et les dendrites ; pour Hameroff et Penrose [16] via les microtubules ; pour Eccles [8] au niveau synaptique.

Le MP au niveau des assemblées de neurones a été déjà mis en évidence par Edelman [9] sous le nom de "principe de dégénérescence" (par analogie avec la "dégénérescence" du code génétique du fait que le même acide aminé peut être codé par deux codons différents).

La mémoire Mem se développe sous l'action collective des différents CR et du jeu entre leurs stratégies. Elle enregistre de manière flexible bien qu'assez stable les diverses expériences du SEM. Elle a un rôle central, puisque ses objets, appelés empreintes, peuvent être perçus par les différents CR sous des aspects différents et avec différentes décompositions; ainsi des CR inférieurs peuvent ne percevoir qu'un certain attribut (par exemple, couleur, forme,…) de l'objet mémorisé.

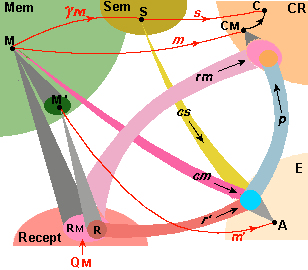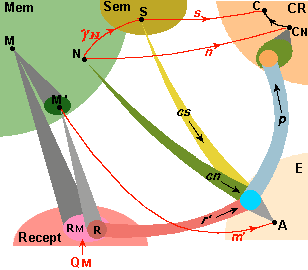
Montrons comment un stimulus externe Q_M sera mémorisé. Dans son paysage, un CR inférieur, disons E, perçoit seulement les aspects r' d'un sous-pattern R des récepteurs correspondant à un attribut particulier (par exemple, couleur) ; R est mémorisé par la formation d'une colimite M' qui représente la E-empreinte de l'événement, éventuellement vue par son aspect m' dans le paysage de E. De la même façon, un CR supérieur qui voit les aspects r_M d'un plus grand pattern de récepteurs R_M formera son empreinte M de Q_M, vue par son aspect m dans le paysage du CR. Par suite du jeu entre les stratégies, M est également la colimite des empreintes (telles que M') formées par les CR inférieurs que le CR supérieur contrôle.

Plus tard si le même stimulus est rencontré à nouveau, l'empreinte peut être rappelée au travers des paysages des différents CR, et être activée par l'intermédiaire de n'importe laquelle de ses ramifications. Les empreintes des stimuli externes (transmis par les récepteurs sensoriels) et de leurs liens forment un sous-système de Mem, appelé la mémoire empirique, et notée Emp. Les stratégies utilisées et leurs résultats sont également enregistrés, et forment un sous-système de Mem appelé la mémoire procédurale, dénotée par Strat ; elle contient des empreintes des différents comportements de l'animal.

Le système neural d'un animal supérieur peut non seulement mémoriser ses expériences de toute nature, mais aussi classifier leurs empreintes en classes d'invariance. Pour modéliser ce processus de classification dans le SEM des neurones, nous supposons que les complexifications successives ajoutent également des limites, appelées CR-concepts, classifiant les classes d'invariance des empreintes selon certains de leurs attributs. Une telle classification exige une réflexion interne, avec des CR inférieurs effectuant une classification "pragmatique', et des CR supérieurs capables "d'interpréter" cette classification et de lui donner une représentation.

En effet, soit E un CR inférieur correspondant à un certain attribut (par exemple couleur) ; un stimulus externe Q_M (ou son empreinte M) active un pattern P d'agents de E, appelé E-trace de M. Deux items sont "agis" comme équivalents par E s'ils ont la même E-trace ; par exemple, dans un couleur-CR, c'est le même pattern de récepteurs qui est activé par tous les objets bleus.

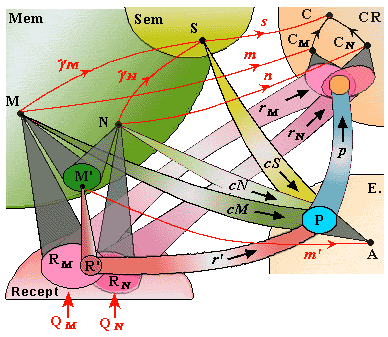Mais cette classification prend sa signification seulement au niveau d'un CR de niveau plus élevé avec une plus longue période, capable de percevoir que différentes empreintes ont la même E-trace (la même couleur), et d'enregistrer ce résultat dans la mémoire sous la forme d'un objet (la couleur "bleu') représentant la classe entière de ces empreintes. Cet objet, appelé le E-concept de M, est construit comme étant la limite* (projective) S de P, vue par son aspect s dans le paysage du CR. Il y a un lien g_M de M vers S, modélisant le fait que M est une instance du concept S.

L'activation du concept S peut activer l'une quelconque de ses instances, avec un va-et-vient possible entre deux instances M et N. De plus la seule activation de M peut activer son concept S qui peut alors activer une autre instance N de S, de ce fait débutant un va-et-vient entre M et N. Les CR-concepts relatifs aux divers CR sont à la racine de la formation, par complexifications successives, de concepts généraux, construits en tant que limites itérées de patterns de CR-concepts. Tout d'abord sont formés des concepts classifiant simultanément plusieurs attributs (e.g. triangle bleu), et puis des concepts plus abstraits obtenus comme limites de patterns de tels concepts "concrets" liés par des liens complexes.

Un concept peut être considéré comme un prototype abstrait pour une classe d'objets ayant une "ressemblance de famille" (au sens de Wittgenstein) ; il ne nécessite pas l'existence d'un langage.

La réactivation ultérieure d'un concept se fonde sur une double indétermination : va-et-vient entre différentes instances du concept, puis balancement complexe entre différentes ramifications de ces instances. Remarquons que ces deux opérations de "balance" sont à caractère quelque peu dual : Le balancement complexe entre deux patterns correspond à une alternative entre deux décompositions non-équivalentes d'un même objet d'ordre supérieur ; le choix de l'un d'eux peut être vu comme étant un analogue classique de la réduction ("collapse") de la fonction d'onde d'une superposition quantique. Le va-et-vient entre deux instances d'un concept correspond à une alternative entre deux présentations différentes des attributs qu'ils ont en commun ; il peut se voir comme étant un analogue classique d'un processus de non-localisation, les attributs étant présentés de manière différente dans les deux instances. (Ce sont ces extensions des propriétés quantiques que Aerts et al. [1] mettent en lumière.) Dans le premier cas, les deux alternatives fusionnent au niveau supérieur ; dans le second, elles apparaissent par dissociation d'une base commune.

Les concepts et leurs liens forment un sous-système de Mem, appelé la mémoire sémantique et dénoté par Sem.

Le développement d'une mémoire sémantique ajoute de la flexibilité au jeu entre les stratégies des CR. En effet, il se formera des concepts représentant des classes d'invariance de stratégies dans la mémoire procédurale Strat, et le choix d'une stratégie par un CR supérieur sera fait sous la forme d'un tel concept, au lieu d'une stratégie spécifique de sa classe d'invariance. Ceci ajoute un nouveau degré de liberté dans la formation de la stratégie globale effectivement réalisée par le système à un moment donné, puisque le jeu entre les stratégies peut choisir parmi les stratégies de la classe d'invariance choisie par un CR celle qui est la mieux adaptée, compte tenu des stratégies transmises par les autres CR. Par exemple, la commande de saisir un objet sera modulée selon l'objet à saisir.

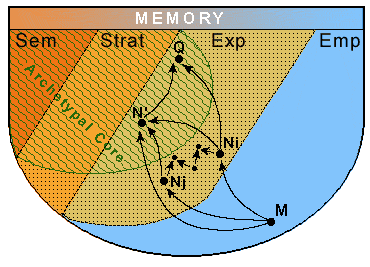
Nous avons vu que la mémoire Mem contient 3 sous-systèmes avec des liens entre eux : la mémoire empirique Emp, la mémoire procédurale Strat, et la mémoire sémantique Sem où les empreintes sont classifiées en concepts. Maintenant nous allons établir une distinction parmi les empreintes selon la différence de leur force, mettant ainsi en évidence 2 autres sous-systèmes de Mem : le noyau archétypal AC et la mémoire expérientielle Exp.

Les empreintes des patterns qui sont activés plus souvent et pendant une plus longue période, à partir de la naissance (par exemple, aspects stables de l'environnement contrairement à ceux plus variables, émotions profondes,…) et leurs liens forment un sous-système particulier de la mémoire, appelé le noyau archétypal, dénoté par AC ("archetypal core"). Il se développe pour intégrer les principales expériences sensorielles, proprioceptives, motrices, états internes …, avec leur coloration émotive, et les relier en patterns aux liens forts, rapidement activés et graduellement renforcés. Il représente une mémoire "affective" personnelle de l'animal, de son corps, de ses expériences, des connaissances acquises qu'elles soient pragmatiques, sociales ou conceptuelles, ainsi que des stratégies de base qui leur sont associées.

Les liens archétypaux peuvent être activés de façon autonome, de sorte que tout un sous-système de AC soit activé dès qu'une petite partie en est stimulée. Et quelles que soient les variations des stimuli cette auto-activation au travers des liens du noyau archétypal peut être maintenue assez longtemps. Elle est engendrée par des suites de boucles basées sur des va-et-vient entre diverses instances de ses concepts et des balancements complexes entre leurs ramifications (dans le système neural, elle repose sur les boucles thalamo-corticales). Par exemple une empreinte dans AC (disons le ciel bleu) est également archétypalement liée à d'autres empreintes, non seulement de perceptions ou de processus moteurs mais également d'états et d'émotions internes (soleil, chaleur, bien-être, nager,…).

Certaines empreintes représentent des expériences qui sont assez significatives pour être reliées par des liens forts au noyau archétypal, mais sans lui appartenir ; celles-ci avec leurs liens forment un sous-système de Mem, appelé la mémoire expérientielle, dénotée par Exp (à comparer à la "value-category memory" de Edelman [9]). Ses objets peuvent représenter des stimuli externes aussi bien que des états internes, des comportements ou des stratégies, ou une association de tels.

Chaque empreinte N dans Exp est liée à un objet "le plus proche" de AC dans le sens que l'activation de N réactive l'expérience archétypale la plus étroitement liée à N, qui diffuse alors l'activation à d'autres expériences liées à celle-ci dans AC, et l'activation s'étend ainsi en boucles qui s'auto-entretiennent longtemps et peut se propager à des aires proches. Formellement, AC est un sous-système réflexif* de Exp au sens suivant : pour chaque N dans Exp, il existe un lien de N vers un objet de AC. par lequel tout autre lien de N à un objet de AC se factorise de manière unique.

Par des complexifications successives dirigées par le réseau des CR, la mémoire se développe et s'étend par formation de nouvelles colimites M qui deviennent des empreintes empiriques ou procédurales. Une telle empreinte est liée par une gerbe à un pattern d'expériences proches N_i dans la mémoire expérientielle. Formellement, Exp est un sous-système final* de Mem. Puisque, comme dit ci-dessus, le noyau archétypal est un sous-système réflexif de Exp, chaque N_i activé par M rappelle également l'empreinte archétypale qui lui est la plus proche N', à partir de laquelle l'activation s'étend à d'autres empreintes Q le long des différents liens du noyau archétypal.

L'organisation de la mémoire est encore précisée par l'identification par un CR d'une identité sémantique entre empreintes, ce qui permet de les classifier en concepts. Si les liens d'une empreinte à Exp deviennent assez forts, elle sera intégrée dans Exp, et probablement aussi plus tard dans le noyau archétypal. Tandis que seulement une partie de la mémoire empirique deviendra expérientielle, l'intégralité de Strat et de Sem se développeront en sous-systèmes de Exp. et, au moins au début, la majorité de Exp est progressivement intégrée dans le noyau archétypal, en priorité les empreintes d'états internes.

Par exemple, le noyau archétypal d'un enfant en bas âge contient déjà un réflexe pour saisir. Il se développera progressivement en une stratégie sensori-motrice bien dirigée pour prendre un objet : un CR visuel apprendra à identifier certains objets (dans Emp), un CR "émotif" rappellera le plaisir (dans AC) de tenir ces objets, un CR moteur rappellera les mouvements pour saisir ces objets (stratégie dans Strat). Quand le bébé identifie un tel objet, les liens entre ces différentes empreintes sont activés, avec des va-et-vient entre les différentes instances des concepts qui leur sont associés, de sorte que ces CR coopèrent par le jeu entre leurs stratégies pour s'efforcer de saisir l'objet. Le bébé apprendra à ajuster ses mouvements selon la taille et la forme de l'objet, et ceci sera mémorisé par la formation d'une colimite représentant l'acte particulier, puis la formation d'un concept archétypal du comportement sensori-moteur général de "saisie d'un objet'.

Nous appuyant sur les résultats ci-dessus et sur ceux de Ehresmann et Vanbremeersch [13], nous proposons de caractériser la conscience comme un processus en 3 parties reposant sur le développement du noyau archétypal qui, toujours en arrière plan, agit en tant que référent et filtre : (i) formation d'un paysage étendu "holiste" sur lequel peut être opérée (ii) une rétrospection vers le passé pour trouver les causes d'un événement, et (iii) une prospection vers le futur pour trouver les stratégies les mieux adaptées. Le degré de conscience dépendra du développement du noyau archétypal : plus il est développé et plus étendu sera le paysage construit, ce qui conduit à une recherche plus profonde dans le passé et à un choix de stratégies à plus long terme. Ces processus sont définis comme suit :

Supposons que, dans le bruit de fond empirique, apparaisse un nouvel événement significatif qui n'a aucune réponse automatique (par exemple, une fracture dans le paysage d'un CR supérieur). Il détermine immédiatement une augmentation de l'attention (activation de la formation réticulaire), ce qui déclenche une recherche sémiotique dans la mémoire via les CR de tous les niveaux (couleur, forme, …) jusqu'à la sémantique pour essayer d'identifier l'évènement, utilisant des processus de va-et-vient entre instances d'un concept et de balancements complexes entre leurs ramifications. En effet, parmi les empreintes ainsi activées certaines forment des patterns admettant la même projection sémantique que des empreintes archétypales ou des expériences non-archétypales dans Exp. Il s'ensuit que les paysages de CR supérieurs perçoivent, pour l'un C1 des aspects venant du noyau archétypal, pour un autre C2 des aspects venant de la mémoire empirique et de la mémoire expérientielle. Comme les deux CR sont reliés par les perspectives des liens entre Emp, Exp et AC, ces CR forment ensemble une perception alternative, ambivalente de l'expérience et du stimulus empirique. Un CR encore supérieur reçoit une alternative, à différents intervalles, des aspects de ces empreintes empiriques, expérientielles et archétypales et de leurs diverses ramifications. Chaque CR agit selon sa propre temporalité ; les alternatives d'origine archétypale par définition sont plus rémanentes, étant réactivées sur une plus grande durée que celles de la mémoire empirique.

(i) De cette façon, des CR supérieurs relient les paysages des différents CR qu'ils contrôlent, en tenant compte des expériences spécifiques du sujet telles qu'elles sont reflétées par le noyau archétypal. Ainsi est formé un paysage étendu "holiste', dont les objets sont les perspectives temporelles de l'événement et de ses réflexions internes, en particulier dans le noay archétypal (à comparer au "Global Workspace model" ou au "théâtre" de Baars [2]). Physiologiquement sa construction se fonde sur l'existence des boucles fonctionnelles entre les diverses parties du cerveau, qui forment ce que Edelman ([9], p. 100) appelle la "boucle de conscience".

(ii) Un processus de rétrospection, basé sur une suite de va-et-vient entre instances et de balancements complexes entre leurs ramifications, sera opéré sur ce paysage étendu ; il permet d"accèder aux niveaux inférieurs du passé proche pour trouver, par abduction, les causes possibles de l'événement actuel.

(iii) Enfin un processus de prospection (orienté vers le futur) choisira des stratégies à long terme pour plusieurs étapes, de sorte à répondre de la manière la plus adaptative. Ceci est accompli par la formation, à l'intérieur du paysage étendu, de paysages virtuels, avec l'aide du noyau archétypal et de la mémoire entière, dans lesquels les stratégies successives (choisies sous forme de concepts) peuvent être "essayées" sans coût matériel pour le système.

Dans ce modèle, l'évolution du noyau archétypal et de la conscience se fonde sur l'existence de va-et-vient entre instances et de balancements complexes entre leurs ramifications, ce qui résulte du MP. Elle prend en compte l'expérience entière, qu'elle soit perceptive, comportementale ou émotive (le rôle des émotions a bien été souligné par Damasio [6]), avec une intégration des dimensions temporelles. La permanence du noyau archétypal, ou du moins sa modification très progressive, serait la base de la notion du "soi". Et pour le "hard problem", les qualia pourraient correspondre aux perspectives des objets du noyau archétypal dans le paysage "conscient" étendu.

L'évolution d'une telle conscience donne un avantage sélectif, puisqu'elle permet de rechercher les causes d'un événement au lieu de ne réagir qu'à ses effets. Et en programmant sur le long terme, des stratégies plus efficaces peuvent être conçues, moins assujetties aux conditions immédiates.

Ceci ne nécessite pas un langage (des animaux supérieurs peuvent avoir une telle conscience). Mais le langage rend les processus plus efficaces, parce que l'information complexe (cat-neurones d'ordre supérieur) peut être stockée sous la forme plus compacte de mots, et plus d'opérations peuvent être effectuées à l'aide de ces mots. La conséquence en est le développement d'une "algèbre des objets mentaux" (au sens de Changeux [4]) plus riche et de processus cognitifs d'ordre supérieur, dépendant fortement des interactions sociales, de la communication et de l'éducation.

• Une catégorie est un (multi)graphe orienté sur lequel est donnée une loi de composition qui associe à 2 flèches successives f: N ® N' et f': N' ® N" une flèche ff': N ® N". Cette composition doit satisfaire 2 axiomes :

(i) Associativité : À chaque chemin de longueur n est associé un composé unique, indépendant de sa 2-2 décomposition;

(ii) Identité : à chaque sommet est associée une flèche fermée dont le composé avec n'importe quelle autre flèche redonne cette flèche.

Les sommets du graphe sont appelés les objets de la catégorie, et ses flèches les morphismes (ou les liens).

Un foncteur partiel d'une catégorie K vers une catégorie K' est une application F d'une sous-catégorie C de K dans K' qui associe à chaque objet N de C un objet F(N) de K et à chaque lien f de N vers N' dans C un lien F(f) de F(N) vers F(N') dans K', de sorte que le composé ff' soit appliqué sur le composé des images de f et de f'.

• Un pattern (ou diagramme) P dans une catégorie est formé par une famille d'objets N_i de la catégorie et de liens distingués entre eux.

Un lien collectif de P vers un objet N' est une famille de liens f_i: N_i ® N' corrélés par les liens distingués du pattern dans le sens que, si g est un lien dans P de N_i vers N_j, alors gf_j = f_i .

P a une colimite (ou limite inductive) s'il existe un objet N tel que :

(i) ("propriété universelle") il existe un lien collectif (c_i) de P vers N ; et

(ii) chaque lien collectif (f_i) de P vers n'importe quel objet N' se recolle en un lien unique f de N vers N' tel que f_i = c_if pour chaque i.

Si un pattern a une colimite, elle est unique (à un isomorphisme près).

La somme (ou coproduit) S de la famille des objets (N_i) est la colimite du pattern constitué par ces objets sans aucun lien distingué. Si cette somme S existe ainsi que la colimite N de P, il y a un morphisme canonique de "comparaison" de S vers N.

La limite (projective) d'un pattern P dans la catégorie K est la colimite du pattern opposé dans la catégorie opposée à K (obtenue en changeant la direction de ses morphismes).

• Si P et P' sont des patterns, une gerbe de P vers P' est une famille maximale de liens des objets de P vers les objets de P' telle que :

(i) Chaque objet de P est lié au moins à un objet de P', et s'il est lié à plusieurs ses liens sont corrélés par un zigzag de liens distingués de P'.

(ii) le composé d'un lien de la gerbe avec un lien distingué de P ou de P' est également dans la gerbe.

Si P et P' admettent des colimites N et N' respectivement dans la catégorie, une gerbe de P vers P' se recolle en un lien unique de N vers N' appelé un lien (P,P')-simple. Le composé de deux liens simples recollant des gerbes adjacentes est toujours un lien simple : si f est (P,P')-simple et si f' est (P',P")-simple, alors leur composé ff' est un lien (P,P")-simple.

Mais le lien (P,P')-simple f pourrait ne pas être (Q,Q')-simple pour d'autres décompositions Q de N et Q' de N'. Deux décompositions P et Q d'un objet N sont dites équivalentes s'il existe une gerbe de P vers Q qui se recolle en l'identité de N, de sorte que cette identité soit un lien (P,Q)-simple. Sinon, nous disons que P et Q sont des décompositions non équivalentes de N.

Un lien complexe est un composé des liens simples liant des gerbes non adjacentes, avec balancements complexes entre les différentes décompositions des objets multiface intermédiaires.

• Un Système Evolutif K est la donnée de : une échelle de temps T, qui est une partie discrète ou non, finie ou non, de l'ensemble des réels positifs ; une catégorie K_t pour chaque instant t de l'échelle de temps ; un foncteur partiel, appelé transition de K_t à K_t' pour chaque t < t'.

Un sous-système L de K est un système évolutif dont l'échelle de temps est un sous-ensemble S de T et dont la catégorie L_s est une sous-catégorie de K_s pour chaque s dans S.

L est un sous-système final de K si S = T et si pour chaque objet N de K_t il existe une gerbe du pattern réduit à N vers le pattern représenté par L_t.

L est un sous-système réflexif de K si S = T et si, pour chaque objet N de K_t il existe un objet N' de L_t et un morphisme h de N vers N' tels que tout morphisme de N vers un objet de L_t se factorise de manière unique par h.

• Dans un système hiérarchique, le MP peut être renforcé comme suit :

(i) Il existe des objets du niveau n+1 qui sont n-multiface, dans le sens qu'ils admettent au moins deux décompositions non équivalentes en patterns du niveau n.

(ii) Un objet du niveau n peut appartenir à plusieurs patterns admettant des colimites différentes au niveau n+1.

• Le paysage actuel d'un CR au temps t est construit comme suit. Un objet B du système a un aspect b pour le CR si b est un lien de B vers un objet (ou agent) du CR ; deux aspects sont dans la même perspective s'ils sont corrélés par un zigzag de liens entre les agents du CR (de sorte qu'ils transmettent la "même" information au CR). Le paysage L est la catégorie dont les objets sont les perspectives venant des objets d'un niveau adjacent au niveau du CR et qui perdurent pendant l'étape actuelle du CR (sa longueur est déterminée par l'échelle de temps du CR). Les morphismes viennent des morphismes dans le système, de sorte qu'il y a un foncteur "distorsion" de L vers le système (il mesure extérieurement de combien est déformée l'information partielle perçue par le CR).

Une étape pour le CR consiste en : formation de son paysage actuel L, choix d'une stratégie sur ce paysage (en utilisant la mémoire), transmission des commandes correspondantes aux effecteurs. Le paysage anticipé à l'étape suivante devrait être la complexification L' de L relativement à cette stratégie. Le CR peut alors évaluer si les objectifs ont été atteints par un foncteur "comparaison" de L' vers le paysage effectifement obtenu à cette étape suivante.

Dans cet article, nous avons proposé un modèle mathématique, basé sur la théorie des catégories, pour les processus d'émergence qui mènent progressivement à l'évolution de l'univers à partir du niveau quantique jusqu'au niveau des organisations complexes et même des êtres conscients. Cette évolution est décrite comme une succession de processus de complexification, dans lesquels des patterns d'objets interagissant sont agrégés pour former de nouveaux objets d'ordre plus élevé prenant leur propre identité complexe (représentés dans le modèle catégorique par la colimite du pattern). Ce que nous essayons d'expliquer est dans quel sens un tel nouvel objet N a des propriétés globales émergentes comparées aux propriétés du pattern P qu'il recolle, c'est-à-dire comparées aux propriétés locales des objets de sa décomposition P.

Au niveau atomique, un atome recolle le pattern constitué par sa configuration électronique en orbitales atomiques. Mais la physique quantique affirme que l'atome a plusieurs telles configurations correspondant à différents niveaux d'énergie ; nous disons que c'est un objet "multiface". Nous affirmons que cette propriété est la clef du problème de l'émergence.

En effet, plus généralement N' est un objet multiface s'il admet des décompositions en 2 patterns, disons P' et R', non équivalents, de sorte qu'il puisse "balancer" entre ces deux décompositions ; ce fait ne peut pas être identifié juste en considérant P' et R', mais dépend de la structure entière du niveau inférieur auquel ils appartiennent (le niveau quantique si N' est un atome). L'existence d'objets multiface entraîne l'existence de deux sortes de liens : un lien (P,P')-simple f de N vers N' ne fait que recoller une gerbe de liens entre les objets des décompositions P de N et P' de N', et donc n'ajoute pas de propriétés "nouvelles" relativement au niveau inférieur. Mais il existe également des liens complexes qui sont des composés de liens simples liant des gerbes non adjacentes, par exemple, un lien de N à N" qui est le composé de f avec un lien (R',P")-simple f' de N' à N", où N' est multiface ; ce lien représente de nouvelles propriétés émergeant au niveau de N et de N", puisqu'il dépend non seulement "localement" des constituants de N et de N" du niveau plus bas (réductionnisme) mais aussi "globalement" de la structure entière de ce niveau plus bas de par l'existence d'un balancement complexe entre P' et R'.

Par un raisonnement catégorique, nous prouvons que, si un système a des objets multiface (nous disons qu'il satisfait le principe de multiplicité MP), il en est de même pour toutes ses complexifications successives, et celles-ci mènent à la formation d'objets ayant des ordres croissants de complexité, reliés par des liens complexes qui représentent, à chaque niveau, de nouvelles propriétés émergentes (dans le sens ci-dessus). Comme le système quantique satisfait le MP, il s'ensuit qu'il en est de même pour tous les systèmes naturels qui ont évolué à partir de lui ou de ses sous-systèmes par complexifications successives.

Dans la section 3, nous avons appliqué ce résultat à certains systèmes autonomes anticipatifs, tels que les systèmes biologiques et plus particulièrement les systèmes cognitifs, modélisés dans le cadre catégorique par les Système Evolutifs à Mémoire (SEM). Les complexifications successives de la catégorie des neurones mènent à l'émergence de processus cognitifs de plus en plus complexes. Rappelant certains de nos articles précédents, nous décrivons le développement d'une mémoire générale, et d'une classification de ses objets (ou empreintes) dans une mémoire sémantique. Et nous cherchons à étudier comment la conscience peut surgir.

La nouvelle idée ici est que l'émergence de la conscience repose sur la formation, à partir de la naissance, d'un sous-système de la mémoire, le noyau archétypal, constitué d'objets multiface, qui intègre les principales expériences sensorielles, proprioceptives, motrices, internes …, avec leurs composantes émotives, et les relie en patterns aux liens forts, rapidement activés et graduellement renforcés. Un nouvel événement déclenche une recherche sémiotique dans le noyau archétypal et dans les empreintes qui lui sont liées, avec va-et-vient entre leurs instances et balancements complexes entre les différentes décompositions de celles-ci. Il mène à la formation d'un paysage étendu holiste, dans lequel sont effectués : un processus de rétrospection vers le passé proche pour trouver les causes de l'événement, et un processus de prospection vers l'avenir pour choisir des stratégies à long terme.

Ainsi la conscience apparaît comme un processus qui tient compte de l'expérience entière du sujet, avec ses aspects multiples, qui intègre les dimensions temporelles, et donne des avantages évolutifs en permettant des réponses mieux adaptées. Elle se fonde sur le niveau quantique, non pas directement comme plusieurs auteurs l'ont suggéré, mais par une longue suite d'étapes, conduisant à l'émergence progressive d'objets de plus en plus complexes pendant l'évolution, émergence qui, comme dit ci-dessus, repose sur le fait que le MP est satisfait dans le système quantique, ce qui entraîne sa satisfaction dans les complexifications qui s'en déduisent.

Nous remercions Jerry Chandler, George Farre et Brian Josephson pour des éhanges stimulants sur des problèmes proches de ceux abordés ici.

1. Aerts, D., D'Hondt, E., Gabora, L., "Why the Disjunction in Quantum Logic is Not Classical", Foundations of Physics 30, Issue 10 (2000).

2. Baars, B. J., In the theatre of consciousness : The workspace of the mind, Oxford University Press, Oxford, 1997.

3. Bunge, M., Treatise of basic Philosophy vol. 4, Reidel, 1979.

4. Changeux, J.-P., L'Homme Neuronal, Fayard, Paris, 1983.

5. Cramer, J. J., "The transactional interpretation of quantum mechanics", Review of Modern Physics 58, 647-688 (1986).

6. Damasio, A., The Feeling of What Happens : Body and Emotion in the Making of Consciousness, Harcourt Brace, New York, 1999.

7. Dubois, D., "Introduction to computing anticipatory systems", in Computing anticipatory systems edited by D. Dubois, CASYS First International Conference, Liège, Belgium, August 11-15, 1997, AIP Conference Proceedings 437, New York, 1998.

8. Eccles, J. C., "Do mental events cause neural events?" Proc. R. Soc. London B 227, 411-428 (1986).

9. Edelman, G.M., The remembered present, Basic Books, 1989.

10. Ehresmann, A.C. & Vanbremeersch, J.-P., "Hierarchical evolutive systems...", Bul. Math. Bio. 49 (1), 13-50 (1987).

11. Idem, "Hierarchical Evolutive Systems", in Proc. 8th International Conference of Cybernetics and Systems, Vol. 1, edited by Manikopoulos, C.N., The NIJT Press, Newark, 1990, pp. 320-327.

12. Idem, "Multiplicity Principle and emergence in MES", Journal of Systems Analysis, Modelling, Simulation 26, 81-117 (1996).

13. Idem, "How to model consciousness in a Memory Evolutive System?", Online (1999) in http://perso.wanadoo.fr/vbm-ehr.

14. Farre, G., "The energetic structure of observation", American Behavorial Scientist 40 (6), 717-728 (1997).

15. Hebb, D.O., The organization of behaviour, Wiley, New York, 1947.

16. Hameroff, S. & Penrose, R., "Orchestrated reduction of quantum coherence in brain microtubules", in Scale in conscious experience : Is the brain too important to be left to specialist to study?, edited by King and Pribram, Lawrence Erlbaum, 1995, pp. 341-274.

17. Kan, D. M., "Adjoint Functors", Trans. Am. Math. Soc. 89, 294-329 (1958).

18. Mac Lane, S., Categories for the working mathematician, Springer, 1971.

19. Malsburg (von der), C., "Binding in models of perception and brain function", Current Opinions in Neurobiology 5, 520-326 (1995).

20. Matsuno, K., Protobiology : Physical basis of Biology, CRC Press, Boca Raton, 1989.

21. Minsky, M., The society of mind, Simon & Schuster, New York, 1986.

22. Paton, R., "Structure and Context in Relation to Integrative Biology", BioSystems, Special edition in memory of Michael Conrad, to appear (2001).

23. Pribram, K.H., "Proposal for a quantum physical basis for selective learning", in Proceedings ECHO IV, edited by G. Farre, 2000, pp. 1-4.

24. Rosen, R., Anticipatory systems, Pergamon, New York, 1985.

25. Thom, R., Esquisse d'une Sémiophysique, InterEditions, Paris, 1988.