It is important to be able to distinguish the components of a natural complex system such as a biological or social system, according to their complexity level (which also reverberates on their temporality). The idea is that a 'complex' component has its own internal organization into cooperating more elementary components, that determines its interactions. For example, the interactions of a protein in a cell depend on its configuration consisting of its atoms, their chemical links and the topological relations which describe the folding of the protein. How to model this situation in a category, where the objects seem to be undifferentiated? The complex object will be modeled by the colimit (or binding) of a pattern of linked objects representing its internal organization.

.

The internal organization of a complex object N will be represented by a pattern formed by its own components and the distinguished links between them ensuring that they act synergically ('matter and form').

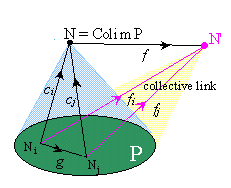
In a category, a pattern P is modeled by the data of a family of objets N_i and of some distinguished links between them. A collective link from the pattern to another object N' is a family of individual links f_i from each N_i to N', correlated by the distinguished links of the pattern, in the sense that, if g is a link in P from N_i to N_j, we have gf_j = f_i .

The collective links model collective actions (constraints, energy, or information transfer) of all the N_i acting in cooperation along their distinguished links, and which could not be realized by the objects of the pattern acting individually. The cooperation can be temporary, as in a group of people who decide to cooperate for a particular work. But the association itself can be represented in the system by a more complex object N, which 'binds' the objects of the pattern and acts by itself as the whole pattern, in the sense that its links to any object N' are in 1-1 correspondence with the collective links from the pattern to N'.

In a category, the object binding the pattern (if it exists) is modeled by the colimit (or inductive limit) of the pattern. An object N is the colimit, or the binding, of the pattern P if it satisfied the two conditions:

If a pattern has a colimit, it is unique (up to an isomorphism). In this case, we also say that the pattern is a coherent assembly and that its colimit represents a higher order object which subsumes the activity of the assembly.

The colimit actualizes the potentiality of the objects to act together in a coherent manner by integrating the pattern in a higher unit (for example, the protein as such). In a natural system where the links have a given 'strength', the formation of a colimit is characterized in two ways:

For example, a molecule is the colimit of the pattern formed by its atoms with the chemical links defining its spatial configuration.

 Decompositions of a complex object

The situation can be seen 'upside-down': if an object N is the colimit of a pattern P, we say that N is a complex object (or as hyperstructure, in the sense of Baas) admitting P as a decomposition. An object may have different decompositions. Indeed, while a pattern has at most one colimit (up to an isomorphism), several patterns may have the same colimit. For instance, the same aminoacid in a protein sequence can be determined by different codons (degeneracy of the genetic code).

Roughly, the colimit forgets the precise organization of the pattern and records only its collective actions, and these can be the same for more or less differing patterns.

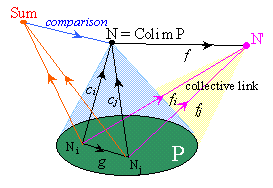
The rôle of the distinguished links of the pattern P is paramount: they determine the 'form' of the colimit and allow for the emergence of collective actions, transcending the individual actions of the objects. The coherence and the constraints introduced by these links can be measured by comparing the colimit to the simple amalgam of the objects N_i of the pattern, obtained if the links are forgotten, which is modeled by their sum.

The sum (or coproduct) S of the family (N_i) is the colimit of the pattern P' formed by these same objects but without any distinguished link. It classifies the individual actions of the objects, while the colimit of the pattern P classifies their collective actions made possible thanks to their distinguished links in P. (Think of the difference between the behavior of an unorganized mob, and the behavior its members adopt under the direction of leaders.)

There is a comparison link c from the sum S of the N_i to the colimit N of P, which binds the canonical links from the N_{i :}to N. It measures the constraints imposed to the objects by their distinguished links, hence by their participation to a collective action. The links from S to an object N' which factor through c correspond to the emergent properties of the complex object N compared to the properties of its components N_i.

For example, the tetramer haemoglobin can be represented as the colimit of the pattern specifying its spatial configuration; the comparison link measures the difference between the oxygenation rate of its 4 separated units and that of the tetramer.