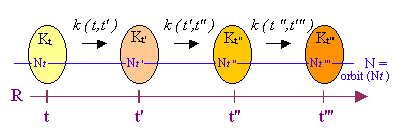Autonomous natural systems, such as biological, social or neural systems, are open in the sense that they have exchanges with their surroundings, and their configuration changes in time, with destruction or rejection of some components, and emergence of new elements, either taken from the outside or internally generated. Thus their dynamical study cannot be confined to that of transformations on a fixed space, whatever be its dimension.
The Evolutive Systems (or ES) introduced in (Ehresmann and Vanbremeersch, 1987) model these systems. They describe the successive configurations of the system at each date of its timescale, and the transformations between them.
The configuration of the system at a time t of its timescale is represented by a category, say Kt, which describes the state of the system at t in the sense of its internal organization as it is defined by its components and their links. It is a 'structural', or relational, notion, and not a spatio-temporal one as in Physics (nearer to Leibniz than to Newton).
The dynamics is characterized by the intrinsic change of the configuration, and not by the motions of its components as seen by an external observer; these motions are taken into account only through their internal consequences, e.g. information or energy transfers (chemical or metabolic reactions).
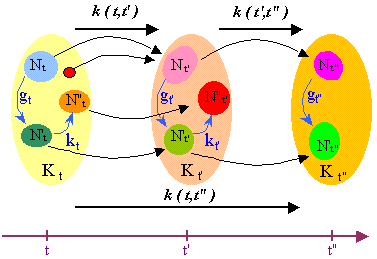
The change from t to t' > t is modelled by a partial functor k(t,t') from the state-category Kt at t to the state-category Kt' at t', called transition from t to t''. (A functor is a map between two categories respecting their graph structures and their composition.)
|
|
The transition specifies what the components and links existing at t have become at t', as we could indicate on two successive photos of an organism how a particular cell has changed. Formally, if an object Nt of Kt has an image by the transition k(t,t'), we say that this image is the new state of Nt at t' and we denote it by Nt' (with the same letter N); if it has no image, we say that Nt is suppressed at t' (death of the cell); and the same for the links. In fact, k(t,t') can be extended into a 'global' functor (instead of a partial one) by supposing that the state-categories have a zero-object 0, and that the suppressed elements are mapped on the zero of Kt'. The transition can be many-to-one, so that two different components at t may have the same state at t'.
To ensure that the successive states of an element, say Nt, are uniquely defined, we assume that the transitions are transitive, in the following sense:
1. If Nt has a new state Nt' at t' and if Nt' has a new state at t">t', then Nt" is also the image of Nt by the transition from t to t".
2. Conversely, if Nt has a state Nt' at t' and a state Nt" at t", then Nt' has a state at t" and this state is Nt". However Nt may have a state Nt" at t" without having a state at t', that means it has temporally disappeared.
Formally, an Evolutive System (or ES) is defined by the following data:
1. its timescale which is a (finite or infinite) subset of the real numbers,
2. for each date t of its timescale, its state-category Kt,
3. for each t' > t, the transition k(t,t') which is a partial functor from Kt to Kt' , these transitions being transitive in the above sense.
|
|
In classical models, a component of a system, say a cell in an organism, is supposed to remain 'the same' at the various times. On the contrary, in an ES, the cell as such is not represented by a unique object, but by the sequence of its successive states. Formally, a component N of the ES is a maximal sequence (Nt) of objects of the state-categories such that, for t' > t, Nt' is the state of Nt at t'. To say that the sequence is maximal means that it contains all the objects correlated by the transitions, but without imposing that N has a state at each time of the timescale of the ES. Indeed, N may appear (birth) later, be suppressed (death) sooner, and even disappear during some periods. For example, in the ES formed by the inhabitants of a country, a man may go to reside in a foreign country and come back later on.