The introduction of categories by Eilenberg and Mac Lane in 1942 aimed to transform difficult problems of Topology into more easy problems of Algebra. Later on, the Theory of categories has been developed, both for itself, and for its applications in various domains of Mathematics (e.g., in Differential Geometry). Even if part of its self-centered development has sometimes been criticized as "abstract non-sense", categories are now recognized as a powerful language for a universal semantics of mathematical structures. They are also used in Logics (through Topos Theory) and in Physics, and in the last years a fruitful cooperation has been established between categoricians and computer scientists (e.g., through Sketch Theory).

Rosen has stressed the interest of categories in Biology as soon as '58 and, following his lead, several authors have used 'large' categories of various systems. The application of categories to natural complex systems which we develop since '86 in the theory of Memory Evolutive Systems is more structural and relies on the theory of colimits and 'completions' of categories.

Roughly, a category is an oriented graph equipped with a law to compose successive arrows, satisfying some axioms.

A graph (also called oriented graph, or diagram scheme, or polygraph) consists of a set of objects, called the vertices of the graph, and a set of arrows between them; if f is such an arrow from A to B, denoted by f : A ® B, we say that A is its source and B its target. Several arrows may have the same source and target (they are said to be 'parallel'), and there may exist 'closed' arrows whose source and target are the same.

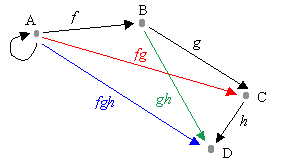
Two arrows f, g are successive, or form a path of length 2, if the target of the first one is the source of the second one:

f: A ® B, g: B ® C.

More generally, a path of length n from A to C is a sequence (f₁,f₂,...,f_n) of n successive arrows:

f₁: A ® A₁, f₂: A₁ ® A₂, ..., f_n: A_n-1 ® C.

A category is a graph in which there is given a composition of arrows which associates to each 2-path (f, g) from A to C an arrow fg of the graph from A to C, called their composite. This composition satisfies the following conditions:

- Associativity. If (f, g, h) is a path of length 3, the two composites f(gh) and (fg)h are equal (denoted by fgh). It follows that any path of length n has also a unique composite.

- Identities: For each vertex A, there exists a closed arrow from A to A, called the identity of A, whose composite with any arrow with source or target A is equal to this other arrow.

The vertices of the graph are also called the objects of the category and its arrows morphisms (or simply links). A morphism f is an isomorphism if there exists a morphism g (called its inverse) such that the composites fg and gf are identities.

In a category, the links are more important than the objects they connect. In fact, the interest of categories resides in the wealth of information on the 'structure' of the objects which can be deduced from the sole analysis of the links and the operations on them.

The state of a natural system, such as a biological, social or neural system, at a given time t can be modeled by a category: its objects represent the components (of any level) of the system, and the morphisms their links in the system at this time. These links may represent more or less stable structural links such as causal or topological relations (e.g., desmosomes between adjacent cells), channels transmitting information, spatial or energetic constraints, or temporary interactions between two components.

The composite of two successive links N ® N' and N' ® N" represents the cumulative interaction from N to N" obtained by taking first the interaction from N to N', then the interaction from N' to N".

Thus an object N plays a double rôle: 1. It acts as an agent, or an emitter, through its links toward the other objects which represent its actions, or the messages it sends. 2. It becomes a receptor, or an observer, through the links toward it, which correspond to the aspects it observes, or the information it receives, or the constraints which are imposed to it.

In a biological system, the identity of an object models its 'self'. The composition of links determines classes of paths which are 'functionnally' equivalent (i.e., with the same practical effect), namely all the paths between two objects having the same composite; it allows to characterize the various temporally and energetically equivalent paths by which an information can be transmitted from a component to another one.

The system may have had some components before the time t which no more figure in it at t. These 'lost' components can be modelled by adding to the category a zero object (or initial object) 0, i.e. an object such that there exists a unique link from 0 to any other object. We say that we have a category with a zero-object.

A group is an example of a 'small' category (with a unique object, namely the unit of the group). An equivalence relation or an order relation on a set E also defines a small category: its objects are the elements of E, and the morphisms are pairs of elements in the relation. On the other hand, mathematical structures of a given type determine 'large' categories: the category of sets and maps between them; the category of topological spaces and continuous maps; the category of groups and their homomorphisms;...; and also the category whose objects are the 'small' categories and the morphisms the functors between them, i.e., the maps preserving the source, target and composition law.